霍夫曼树

树的带权路径长度

设二叉树具有 $n$个带权叶结点，从根结点到各叶结点的路径长度与相应叶节点权值的乘积之和称为 树的带权路径长度（$\text{Weighted Path Length of Tree，WPL}$）。

设$w_i$为二叉树第$i$ 个叶结点的权值，$l_i$ 为从根结点到第 $i$ 个叶结点的路径长度，则 $\text{WPL}$ 计算公式如下：

$$WPL=\sum_{i=1}^nw_il_i$$

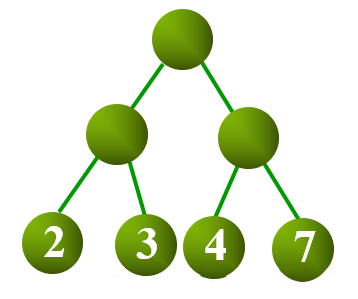
如上图所示，其 $\text{WPL}$ 计算过程与结果如下：

$WPL=2*2+3*2+4*2+7*2=4+6+8+14=32$

对于给定一组具有确定权值的叶结点，可以构造出不同的二叉树，其中，$\text{WPL}$ 最小的二叉树 称为 霍夫曼树（$\text{Huffman Tree}$）。

对于霍夫曼树来说，其叶结点权值越小，离根越远，叶结点权值越大，离根越近，此外其仅有叶结点的度为 $0$，其他结点度均为 $2$。

霍夫曼算法

霍夫曼算法用于构造一棵霍夫曼树，算法步骤如下：

1. 初始化：由给定的 $n$ 个权值构造 $n$ 棵只有一个根节点的二叉树，得到一个二叉树集合$F$。
2. 选取与合并：从二叉树集合 $F$ 中选取根节点权值 最小的两棵 二叉树分别作为左右子树构造一棵新的二叉树，这棵新二叉树的根节点的权值为其左、右子树根结点的权值和。
3. 删除与加入：从 $F$ 中删除作为左、右子树的两棵二叉树，并将新建立的二叉树加入到 $F$ 中。
4. 重复 $2$、$3$ 步，当集合中只剩下一棵二叉树时，这棵二叉树就是霍夫曼树。

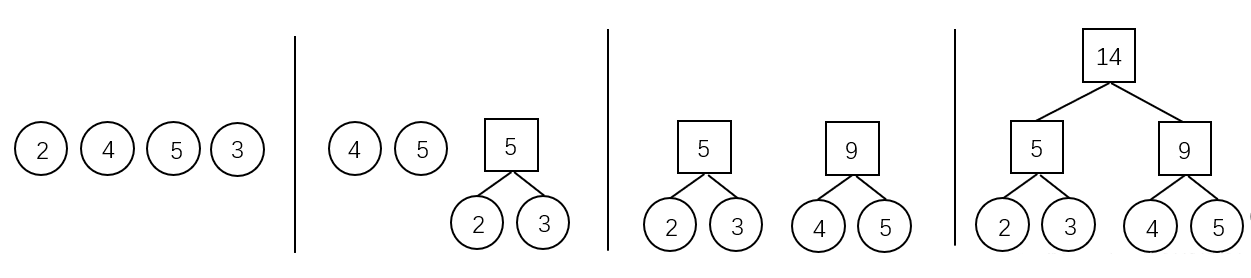
霍夫曼编码

在进行程序设计时，通常给每一个字符标记一个单独的代码来表示一组字符，即 编码。

在进行二进制编码时，假设所有的代码都等长，那么表示$n$ 个不同的字符需要 $\left \lceil \log_2 n \right \rceil$位，称为 等长编码。

如果每个字符的 使用频率相等，那么等长编码无疑是空间效率最高的编码方法，而如果字符出现的频率不同，则可以让频率高的字符采用尽可能短的编码，频率低的字符采用尽可能长的编码，来构造出一种 不等长编码，从而获得更好的空间效率。

在设计不等长编码时，要考虑解码的唯一性，如果一组编码中任一编码都不是其他任何一个编码的前缀，那么称这组编码为 前缀编码，其保证了编码被解码时的唯一性。

霍夫曼树可用于构造 最短的前缀编码，即 霍夫曼编码（$\text{Huffman Code}$），其构造步骤如下：

1. 设需要编码的字符集为：$d_1,d_2,\dots,d_n$，他们在字符串中出现的频率为：$w_1,w_2,\dots,w_n$。
2. 以 $d_1,d_2,\dots,d_n$ 作为叶结点，$w_1,w_2,\dots,w_n$ 作为叶结点的权值，构造一棵霍夫曼树。
3. 规定哈夫曼编码树的左分支代表 $0$，右分支代表 $1$，则从根结点到每个叶结点所经过的路径组成的 $0$、$1$ 序列即为该叶结点对应字符的编码。

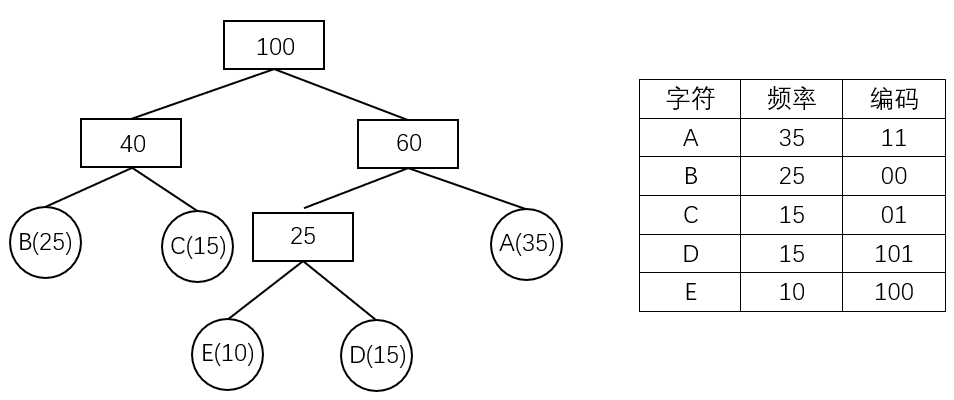
例题

荷马史诗

这个题不难看出是 $k$ 叉哈夫曼树，那么 $k$ 叉哈夫曼树在构造的时候，大体和我们二叉是一样的，不难发现二叉就是每次选两个权值最小的点，然后生成一个新的节点，然后继续寻找这个过程，很想合并果子那个题？

这里 $k$ 叉哈夫曼树也类似，不过有一些特例，这里我们等价于每次一定选择 $k$ 个节点，然后生成一个新节点，但是有可能剩余的节点不够$k$个，导致无法选择？

这个时候容易发现，继续按照这个思路贪心是可以举出反例的，因为我们可以把前面构造好的权值大的点，拉上来降低深度，就降低了 $WPL$.

所以正确做法是首先判断 $(n-1)\%(k-1)$ 是否等于 $0$。

解释：

首先我们每次选 $k$ 个，然后生成一个，相当于每次减少 $k-1$ 个点，为何是 $n-1$ ，因为最后那个点当根节点去了，不需要再进行新一轮选择。

那么如果不等于 $0$ ，我们可以人为的添加一些权值为 $0$ 的点，以此满足 $(n-1)\%(k-1)==0$ ,那么添加多少呢？

不难计算出是 $k-1-mod$,$mod$ 就是上面式子的余数。

流程：

1. 初始节点都入堆(小根堆)，维护每个点的点权和深度初始化所有点深度为 $1$ ，上面点的深度大，相当于倒过来看整棵树。
2. 每次取出堆顶 $k$ 个点，计算权值和，同时维护取出点的最大深度
3. 将计算的权值和，和最大深度加 $1$ 。重新入堆，相当于创造出了一个新节点。
4. 最后输出权值和以及根的深度就是我们这个题的需求了。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5 + 5;
ll n, k, w[N], ans;
struct node
{
    ll w, h;
    bool operator < (const node &x) const
    {
        if (w != x.w) return w > x.w;
        return h > x.h;
        //因为我们是按照最低层当深度1，所以自然是取深度低的点
    }
};
priority_queue<node> q;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n >> k;
    for (int i = 1; i <= n; i++)
    {
        cin >> w[i];
        q.push({w[i], 1});
    }
    if ((n - 1) % (k - 1) != 0)
    {
        int mod = (n - 1) % (k - 1);
        for (int i = 1; i <= k - 1 - mod; i++)
        {
            q.push({0, 1});//补充一些权值为0的点，深度也都为1
        }
    }
    while (q.size() != 1)
    {
        node tmp;
        ll sum = 0, maxh = 0;
        for (int i = 1; i <= k; i++)
        {
            tmp = q.top();
            q.pop();
            sum += tmp.w;
            maxh = max(maxh,tmp.h);
        }
        ans += sum;
        q.push({sum, maxh + 1});//新节点入堆
    }
    cout << ans << "\n" << q.top().h - 1;
    return 0;
}

看题解区大佬挺多，甚至源老师都来了，那蒟蒻也来水一发吧！

对于本题来说，每次从队中选出权重最小的 $k$ 个节点，将其合并建边，然后放回堆中，知道建立玩哈夫曼树。

不过需要注意的是，每次合并都会减少 $k - 1$ 个节点，在合并最后一次的时候，如果可以合并的点的数量不足 $k$ 个，靠近根节点的位置（段编码）反而没有被利用，所以需要补上 $k - 1 - (n - 1)$ 个权重为 $0$ 的结点，把有权重的结点“推”到离根节点更近的位置。

但是，十年OI一场空，不开long long见祖宗啊！

$AC~Code:$

#include <bits/stdc++.h>
#define ll long long
#define IOS ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
using namespace std;
int n, k;
ll ans, x;
struct T
{
    ll w, h;
};
bool operator <(T a, T b)    // 关系运算符重载
{
    if (a.w != b.w)
        return a.w > b.w;  // 如果权重相同，高度小的优先
    return a.h > b.h;
}
priority_queue<T> q;
int main()
{
    IOS;  // 读入加速
    cin >> n >> k;
    for (int i = 1; i <= n; i++)
    {
        cin >> x;
        q.push({x, 1});  // 读入结点
    }
    if ((n - 1) % (k - 1) != 0)  // 如果最后不够
        for (int i = 1; i <= k - 1 - (n - 1) % (k - 1); i++)
            q.push({0, 1});  // 需要补权重为 0 的结点的个数
    while (q.size() != 1)
    {
        T tmp;
        ll sum = 0, maxn = 0;
        for (int i = 1; i <= k; i++)  // 找 k 次最小的
        {
            tmp = q.top();
            sum += tmp.w;  // 新结点加上子结点权重
            maxn = max(maxn, tmp.h);  // 最大深度
            q.pop();
        }
        ans += sum;  // 统计答案贡献
        q.push({sum, maxn + 1});  // 放回去
    }
    cout << ans << endl << q.top().h - 1 << endl;  // 编码长度是高度减一
    return 0;
}

这个代码将结构体 T，也就是哈夫曼数的结点，作为优先队列中的元素；同是重载了小于号运算符，用于比较两个节点谁的权值更小；如果权值一样，则高度更低的节点优先。

#define ll long long
using namespace std;
const int N = 1e5 + 5;
ll n, k, w[N], ans;
struct node
{
    ll w, h;
    bool operator < (const node &x) const
    {
        if (w != x.w) return w > x.w;
        return h > x.h;
    }
};
priority_queue<node> q;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n >> k;
    for (int i = 1; i <= n; i++)
    {
        cin >> w[i];
        q.push({w[i], 1});
    }
    if ((n - 1) % (k - 1) != 0)
    {
        int mod = (n - 1) % (k - 1);
        for (int i = 1; i <= k - 1 - mod; i++)
        {
            q.push({0, 1});
        }
    }
    while (q.size() != 1)
    {
        node tmp;
        ll sum = 0, maxh = 0;
        for (int i = 1; i <= k; i++)
        {
            tmp = q.top();
            q.pop();
            sum += tmp.w;
            maxh = max(maxh,tmp.h);
        }
        ans += sum;
        q.push({sum, maxh + 1});
    }
    cout << ans << "\n" << q.top().h - 1;
    return 0;
}

#include <bits/stdc++.h> #define ll long long using namespace std; const int N = 1e5 + 5; ll n, k, w[N], ans; struct node { ll w, h; bool operator < (const node &x) const { if (w != x.w) return w > x.w; return h > x.h; //因为我们是按照最低层当深度1，所以自然是取深度低的点 } }; priority_queue<node> q; int main() { ios::sync_with_stdio(false); cin.tie(0); cin >> n >> k; for (int i = 1; i <= n; i++) { cin >> w[i]; q.push({w[i], 1}); } if ((n - 1) % (k - 1) != 0) { int mod = (n - 1) % (k - 1); for (int i = 1; i <= k - 1 - mod; i++) { q.push({0, 1});//补充一些权值为0的点，深度也都为1 } } while (q.size() != 1) { node tmp; ll sum = 0, maxh = 0; for (int i = 1; i <= k; i++) { tmp = q.top(); q.pop(); sum += tmp.w; maxh = max(maxh,tmp.h); } ans += sum; q.push({sum, maxh + 1});//新节点入堆 } cout << ans << "\n" << q.top().h - 1; return 0; }