解题思路

可以把上面的数表右转45度，成一金字塔形状，如下所示：

1/1

2/1 1/2

3/1 2/2 1/3

4/1 3/2 2/3 1/4

…… …… …… ……

该金字塔第1行有1个数，第2行有2个数，…，第i行有i个数。并且第i行上的i个分数的分子从i ~ 1，分母从1 ~ i，即第1个分数为i/1，最后一个分数为1/i。

为输出数表中的第N项，先需计算这一项在第几行。设第N项在x行，由于前x-1行共有1+2+3+…+（x-1）项，前x行有1+2+…+x项，因此有：

可以用一个循环计算第n项所在的行数，如下：

for (i=1; i*(i+1)/2<n; i++);

循环退出后，i*(i+1)/2刚好大于或等于n，因此，i就是第n项所在的行。

第n项在第i行中属于第几项又可以计算出来，公式为：

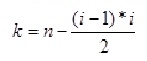即n减去前i-1行中的全部项数。

由于是以z字型方法给数表的每项编号，因此当行号为奇数时，编号从左往右进行；当行号为偶数时，编号从右往左进行。

这样，当i为奇数时，第i行的第k项为（i+1-k）/（k）；当i为偶数时，第i行的第k项为（k）/（i+1-k）。

AC代码

#include <bits/stdc++.h>
using namespace std;
int main()
{
    int i, x, n;
    cin >> n;
    for (i = 1; i * (i + 1) / 2 < n; i++); //不要忘记这个分号!
    x = n - (i * (i - 1) / 2);
    if (i % 2 != 0)
       printf("%d/%d\n", i + 1 - x, x);
    else
       printf("%d/%d\n", x, i + 1 - x);
    return 0;
}

题解

思路1

这道题我很久之前做过，那时我还是萌新时代，啃了10年天，然后终于AC了。

我的思路很简单，直接暴力模拟（这道题就是考模拟，$1 \le n \le 10^7$），我的模拟就是模拟 $n - 1$ 次Z字形移动，判断是否到边上和奇数偶数边，费了老死劲了，才搞出来。

#include <bits/stdc++.h>
using namespace std;
int n, x = 1, y = 1;
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n - 1; i++)
    {
        if ((x + y) % 2 == 0 && y == 1)
        {
            // 向右
            x++;
        }
        else if ((x + y) % 2 == 1 && x == 1)
        {
            // 向下
            y++;
        }
        else if ((x + y) % 2 == 1 && x != 1)
        {
            // 向左下走
            x--;
            y++;
        }
        else if ((x + y) % 2 == 0 && y != 1)
        {
            // 向右上走
            y--;
            x++;
        }
    }
    printf("%d/%d\n", y, x);
    return 0;
}

没啥可说的，看懂了几个if，你就看懂了思路1。

时间复杂度 $O(n)$，能过 $n \le 10^7$。

思路2

现在的我（也不算dalao）当然不屑于简单的暴力，于是我们写了个数学推导优化了模拟！

好吧，其实也没优化多少……

我们发现，在Z字形的边中移动可以省略一部分，这样就会快很多。

我们可以在向左下和右上时直接走到 $x = 1$ 或 $y = 1$，定义一个变量 $step$ 用于记录接下来一下子跳过多少步，让 $i, x, y$ 通过 $+=$ 和 $-=$ 来省略一遍一遍的 $++$ 和 $--$。 但是还有一个问题就是每次 $i += step$ 之后，for循环还会执行 $i++$，我们需要一个 $i--$ 与之抵消。

我们还没有考虑每次快速跳过可能会把答案也给跳过，导致 $i$ 一下子大于了 $n - 1$。 这个问题有两个解决办法，我都会予以出示：

1. 老老实实，在可能超过时一点一点 $++$、$--$。
2. 直接跳到答案。

我们先来看第一个解法：

#include <bits/stdc++.h>
using namespace std;
int n, x = 1, y = 1, step;
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n - 1; i++)
    {
        if ((x + y) % 2 == 0 && y == 1)
        {
            x++;
        }
        else if ((x + y) % 2 == 1 && x == 1)
        {
            y++;
        }
        else if ((x + y) % 2 == 1 && x != 1)
        {
            step = x - 1;
            if (i + step >= n)
            {
                // 如果超了，就正常++、--
                x--;
                y++;
                continue;
            }
            i += step; // 直接跳过 step 步
            i--; // 与for循环多余的i++抵消
            x -= step;
            y += step;
        }
        else if ((x + y) % 2 == 0 && y != 1)
        {
            step = y - 1;
            if (i + step >= n)
            {
                // 如果超了，就正常++、--
                y--;
                x++;
                continue;
            }
            i += step; // 直接跳过 step 步
            i--; // 与for循环多余的i++抵消
            y -= step;
            x += step;
        }
    }
    printf("%d/%d\n", y, x);
    return 0;
}

另一种也很简单，把 $step$ 改成正好到达的方法即可。

#include <bits/stdc++.h>
using namespace std;
int n, x = 1, y = 1, step;
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n - 1; i++)
    {
        if ((x + y) % 2 == 0 && y == 1)
        {
            x++;
        }
        else if ((x + y) % 2 == 1 && x == 1)
        {
            y++;
        }
        else if ((x + y) % 2 == 1 && x != 1)
        {
            step = x - 1;
            if (i + step >= n)
            {
                step = (n - 1) - i + 1; // 计算step
            }
            i += step; // 直接跳过 step 步
            i--; // 与for循环多余的i++抵消
            x -= step;
            y += step;
        }
        else if ((x + y) % 2 == 0 && y != 1)
        {
            step = y - 1;
            if (i + step >= n)
            {
                step = (n - 1) - i + 1; // 计算step
            }
            i += step; // 直接跳过 step 步
            i--; // 与for循环多余的i++抵消
            y -= step;
            x += step;
        }
    }
    printf("%d/%d\n", y, x);
    return 0;
}

计算 $step$ 的时候多看几遍，理解一下。

思路3

发现第 $i$ 条斜线（即分子分母之和 $= i + 1$ 的所有项）中包含 $i*(i-1)/2+1$ 到 $i*(i+1)$ 中的每一项，所以可以二分答案分子分母之和，再根据分子分母之和的奇偶性直接计算第 $n$项

#include <bits/stdc++.h>
using namespace std;
long long n, l, r, mid, ans, x, y; // 需要开long long
int main()
{
    scanf("%d", &n);
    l = 1, r = n;
    while (l < r)
    {
        mid = (l + r) / 2;
        if (mid * (mid + 1) / 2 < n) l = mid + 1;
        else r = mid;
    }
    ans = n - l * (l - 1) / 2;
    // 判断到哪一个方向上了
    if (l % 2 == 0) y = ans, x = l - ans + 1;
    else y = l - ans + 1, x = ans;
    printf("%d/%d\n", y, x);
    return 0;
}

思路4

我们能不能通过公式 $O(1)$ 解决呢？答案是肯定的。

我们将 $Cantor$ 表斜过来看：

$1/1$ $2/1\qquad1/2$ $3/1\qquad2/2\qquad1/3$ $4/1\qquad3/2\qquad2/3\qquad1/4$ $5/1\qquad4/2\qquad3/3\qquad2/4\qquad1/5$

我们发现前 $i$ 行可以理解为一个三角形，而其中包含了 $\frac{i \times (i + 1)}{2}$ 个数。

我们不妨让：

$$\frac{(a - 1) \times a}{2} < n \le \frac{a \times (a + 1)}{2}$$

再让小数 $x$ 满足：

$$\frac{x \times (x + 1)}{2} = n$$

这样我们可知 $a = \lceil x \rceil$。

接下来用求根公式求出 $x$，然后向上取整得到行数 $a$：

$$a = \lceil \frac{-1 + \sqrt{1 + 8 \times n}}{2} \rceil$$

注意这里省去了 $\pm$ 情况中的 $-$，因为 $a > 0$。

接下来还要求出位于这一行的第几个。我们首先知道到了 $a$ 行开始已经过去了几个数：$\frac{(a - 1) \times a}{2}$，那么他就位于：

$$b = n - \frac{(a - 1) \times a}{2}$$

我们还知道，位于第 $a$ 行的所有数，分子分母相加等于 $a + 1$。而通过观察：奇数行分母从 $1$ 开始（按照顺序蛇形），第 $b$ 个分母为 $b$，分子为 $a + 1 - b$；偶数行则分子从 $1$ 开始，分子为 $b$，分母为 $a + 1 - b$。

这样我们就得到了推算方法：

$$a = \lceil \frac{-1 + \sqrt{1 + 8 \times n}}{2} \rceil$$

$$b = n - \frac{(a - 1) \times a}{2}$$

$$y = \left\{ \begin{aligned} &a + 1 - b \qquad \qquad (a \ mod \ 2 = 1)\\ &b \qquad \qquad \qquad \ \ \ \ \ \ (a \ mod \ 2 = 0) \end{aligned} \right.$$

$$x = \left\{ \begin{aligned} &b \qquad \qquad \qquad \ \ \ \ \ \ (a \ mod \ 2 = 1)\\ &a + 1 - b \qquad \qquad (a \ mod \ 2 = 0) \end{aligned} \right.$$

答案为 $y/x$。

虽然是数学推导，我们这里还是把代码写出来。

#include <bits/stdc++.h>
using namespace std;
int n, a, b, y, x;
int main()
{
    scanf("%d", &n);
    a = ceil((sqrt(8.0 * n + 1) - 1) / 2);
    b = n - (a - 1) * a / 2;
    if (a % 2 == 1)
    {
        y = a + 1 - b;
        x = b;
    }
    else
    {
        y = b;
        x = a + 1 - b;
    }
    printf("%d/%d\n", y, x);
    return 0;
}

这里最后再说一句，如果是自己用二分实现的平方根，速度和二分法一样，但是系统的二分比我们快一点，所以时间复杂度可近似 $O(1)$，其实还有很多方法可以求平方根：

1. 二分法 $O(logn)$
2. 牛顿迭代法 $O(loglogn)$
3. 神操作 $O(1)$ 接下来介绍一下神操作的代码：

float InvSqrt(float x) // 平方根的倒数
{
    float xhalf = 0.5f * x;
    int i = *(int*) &x;
    i = 0x5f3759df - (i >> 1);
    x = *(float*) &i;
    x = x * (1.5f - xhalf * x * x);
    return x;
}
float Sqrt(float x) // 平方根
{
    return 1.0 / InvSqrt(x);
}

其他

除此之外，这道题还有很多方法。这里只介绍了4种，其他的就先不介绍了。

$AC$ $Code$ $1$

#include <bits/stdc++.h>
using namespace std;
int n, x = 1, y = 1;
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n - 1; i++)
    {
        if ((x + y) % 2 == 0 && y == 1)
        {
            x++;
        }
        else if ((x + y) % 2 == 1 && x == 1)
        {
            y++;
        }
        else if ((x + y) % 2 == 1 && x != 1)
        {
            x--;
            y++;
        }
        else if ((x + y) % 2 == 0 && y != 1)
        {
            y--;
            x++;
        }
    }
    printf("%d/%d\n", y, x);
    return 0;
}

$AC$ $Code$ $2 \ \ 1$

#include <bits/stdc++.h>
using namespace std;
int n, x = 1, y = 1, step;
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n - 1; i++)
    {
        if ((x + y) % 2 == 0 && y == 1)
        {
            x++;
        }
        else if ((x + y) % 2 == 1 && x == 1)
        {
            y++;
        }
        else if ((x + y) % 2 == 1 && x != 1)
        {
            step = x - 1;
            if (i + step >= n)
            {
                x--;
                y++;
                continue;
            }
            i += step;
            i--;
            x -= step;
            y += step;
        }
        else if ((x + y) % 2 == 0 && y != 1)
        {
            step = y - 1;
            if (i + step >= n)
            {
                y--;
                x++;
                continue;
            }
            i += step;
            i--;
            y -= step;
            x += step;
        }
    }
    printf("%d/%d\n", y, x);
    return 0;
}

$AC$ $Code$ $2 \ \ 2$

#include <bits/stdc++.h>
using namespace std;
int n, x = 1, y = 1, step;
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n - 1; i++)
    {
        if ((x + y) % 2 == 0 && y == 1)
        {
            x++;
        }
        else if ((x + y) % 2 == 1 && x == 1)
        {
            y++;
        }
        else if ((x + y) % 2 == 1 && x != 1)
        {
            step = x - 1;
            if (i + step >= n)
            {
                step = (n - 1) - i + 1;
            }
            i += step;
            i--;
            x -= step;
            y += step;
        }
        else if ((x + y) % 2 == 0 && y != 1)
        {
            step = y - 1;
            if (i + step >= n)
            {
                step = (n - 1) - i + 1;
            }
            i += step;
            i--;
            y -= step;
            x += step;
        }
    }
    printf("%d/%d\n", y, x);
    return 0;
}

$AC$ $Code$ $3$

#include <bits/stdc++.h>
using namespace std;
long long n, l, r, mid, ans, x, y;
int main()
{
    scanf("%d", &n);
    l = 1, r = n;
    while (l < r)
    {
        mid = (l + r) / 2;
        if (mid * (mid + 1) / 2 < n) l = mid + 1;
        else r = mid;
    }
    ans = n - l * (l - 1) / 2;
    if (l % 2 == 0) y = ans, x = l - ans + 1;
    else y = l - ans + 1, x = ans;
    printf("%d/%d\n", y, x);
    return 0;
}

$AC$ $Code$ $4$

#include <bits/stdc++.h>
using namespace std;
int n, a, b, y, x;
int main()
{
    scanf("%d", &n);
    a = ceil((sqrt(8.0 * n + 1) - 1) / 2);
    b = n - (a - 1) * a / 2;
    if (a % 2 == 1)
    {
        y = a + 1 - b;
        x = b;
    }
    else
    {
        y = b;
        x = a + 1 - b;
    }
    printf("%d/%d\n", y, x);
    return 0;
}