题前吐槽

原来的旧题解还能有一个赞也很惊讶…

题解

木棍所构成的长方形的周长（长加宽）是固定的，而面积却有不同，这是为什么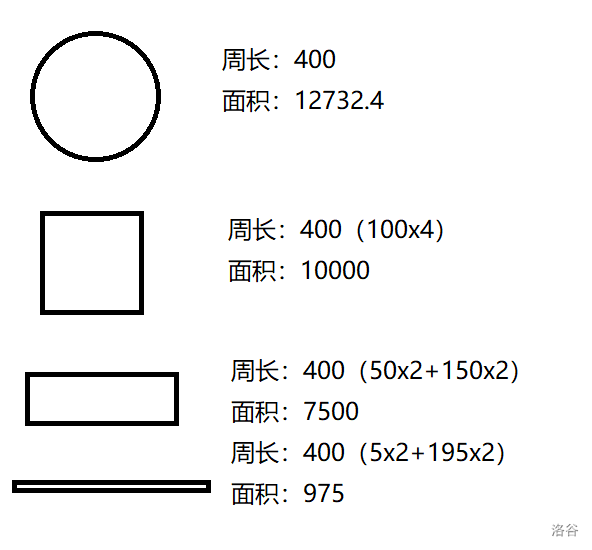？ 我们找到了几个周长相同，但是形状不同的图形，发现面积也不相同。

这个图形越接近棱角平和边缘接近，其面积就越大。 如果我们把长方形的宽拉成 $1$ 纳米，它的长度就会达到周长的一半，而面积就会变得极其小。

反过来如果固定面积，那么边长越接近，图形周长越小： 如果我们只关注长正方形，就会发现：同等周长下，正方形面积最大，接着是长宽差一点的长方形，慢慢长宽差变大，长宽距离悬殊之时面积最小。

这样一来我们就获得了一句至理名言：“和一定差小积大”。

首先“和一定”就是长宽之和固定，差距越小，两者乘积越大。

转移回到这道题上，既然和一定了，我们要把木棍分配给长和宽，尽量让其差值小，就可以达到面积大的目的。所以考察的就是如何合理分配长和宽。

首先一种简易的想法就是一个给长，一个给宽，如此反复。比如输入样例 $2$：2+2=4,2=2，但是输入样例 $1$ 就有错了：2+4=6,3=3，得数 $18 \le 4 \times 5$。所以问题很明显。

接下来就是贪心，把数值给尽量小一点的长或宽。但是仔细检查仍会出错。例如输入 1 1 4 5 1 4，1给长，1（第二个）给宽，4给长，5就给了宽，1给长，4给长，此时两者相差4。所以我们需要给输入的顺序排序。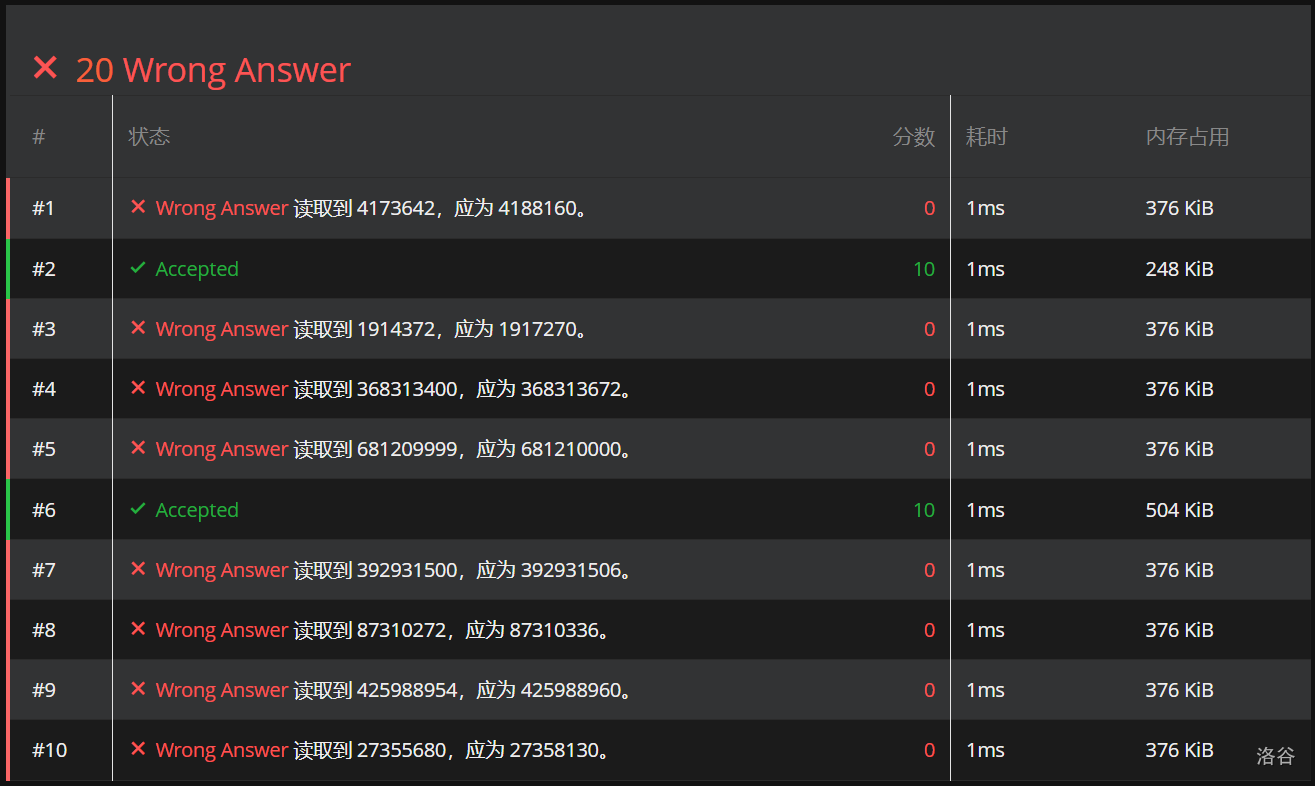 喜提20pts

这道题的正解在于 $DP$，就是那个臭名昭著使人闻风丧胆的动态规划。

观察整个长宽和，发现有奇有偶，偶数期望能平分，奇数期望分出向上取整的一半。而我们为了使得长能够达到期望，就要进行** $01$ 背包**，价值和体积是木棍长度，背包容量是我们的期望。

#include <bits/stdc++.h>
using namespace std;
int n, V, a[105], f[105][100005], sum;
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", a + i);
        sum += a[i];
    }
    V = sum / 2; // 目标
    return 0;
}

就这样写一个简单的 $01$ 背包：

#include <bits/stdc++.h>
using namespace std;
int n, V, a[105], f[105][100005], sum;
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", a + i);
        sum += a[i];
    }
    V = sum / 2; // 目标
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= V; j++) // 不压缩了
        {
            if (j >= a[i])
                f[i][j] = max(f[i - 1][j], f[i - 1][j - a[i]] + a[i]);
            else
                f[i][j] = f[i - 1][j];
        }
    }
    // 结束答案 f[n][V] 表示我们最多凑到 f[n][V]，再也不能更多了，而另一个边长就是 sum - f[n][V]，这个肯定能保证凑出来。
    // 结果自然就是 f[n][V] * (sum - f[n][V])
    printf("%d\n", f[n][V] * (sum - f[n][V]));
    return 0;
}

$AC$ $Code$

#include <bits/stdc++.h>
using namespace std;
int n, V, a[105], f[105][100005], sum;
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", a + i);
        sum += a[i];
    }
    V = sum / 2;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= V; j++)
        {
            if (j >= a[i])
                f[i][j] = max(f[i - 1][j], f[i - 1][j - a[i]] + a[i]);
            else
                f[i][j] = f[i - 1][j];
        }
    }
    printf("%d\n", f[n][V] * (sum - f[n][V]));
    return 0;
}

一点也不基础的动态规划

动态规划真的一生之敌，太弱了

还是和老师对线好久 感谢老师不高血压之恩

状态转移方程

f[ i ][ ia ] = max( f[ i ][ ia ] , f[ i - 1 ][ ia - v[ i ] ] + v[ i ] )

几何定理

当矩形周长一定时，面积最大的情况一定是正方形

完整代码

#include <bits/stdc++.h>
using namespace std;
int f[ 101 ][ 100001 ], v[110] , m , n , a ;
int main()
{
    cin >> n ;
    for (int i = 1; i <= n; i++)
    {
        cin >> v[ i ] ;
        m += v[ i ] ;
    }
    a = m ;
    m /= 2 ;
    m = floor( m ) ;
    for (int i = 1; i <= n; i++)
    {
        for( int ia = 0 ; ia <= m ; ia ++ ) f[ i ][ ia ] = f[ i - 1 ][ ia ] ;
        for ( int ia = v[ i ] ; ia <= m ; ia ++ )
        {
            f[ i ][ ia ] = max( f[ i ][ ia ] , f[ i - 1 ][ ia - v[ i ] ] + v[ i ] ) ;
        }
    }
    cout << f[ n ][ m ] * ( a - f[ n ][ m ] ) ;
    return 0;
}

01背包的简单变化题

这道题就是01背包的简单变化，

01背包模板代码

#include <bits/stdc++.h>
using namespace std;
int m,n,dp[100005],w[105],c[105];
int main()
{
    cin>>m>>n;
    for (int i=1;i<=n;i++)
        cin>>w[i]>>c[i];
    for (int i=1;i<=n;i++){
        for (int j=m;j>=w[i];j--){
            dp[j]=max(dp[j],dp[j-w[i]]+c[i]);
        }
    }
    cout<<dp[m];
    return 0;
}

我们发现01背包有那么几个元素

1. 背包能装的公斤数。
2. 每个物品的重量。
3. 每个物品的价值。

而这几个元素在这道题都有代替 。

1. n根木棍的长度之和。 你想啊，01背包模板中装物品消耗的是载重，这道题一条边加木棍消耗的是总长，这不一样嘛。
2. 每根木棍的长度。
3. 同样是每根木棍的长度。

• 你想，01背包模板里有两个值：剩余载重，总价值，两个是你增我减，你减我增的。因为不同的物品相应增加的价值，减少的载重是不同的，所以，我们才要输入两个值：1 消耗的载重、2 增加的价值。
• 而这里的长、宽就是01背包的这两个值，不同的是，这里”消耗的载重、增加的价值“相同，也就是两个值的增减相同，所以输入一次即可。

当你知道了这些，就可以轻易的用01背包的模板套了。

AC代码（求赞）

#include <bits/stdc++.h>
using namespace std;
int m,he,n,dp[100005],a[105];
int main()
{
    cin>>n;
    for (int i=1;i<=n;i++)
    {
        cin>>a[i];
        he+=a[i];//计算模板中的“背包载重”。
    }
    for (int i=1;i<=n;i++){
        for (int j=he;j>=a[i];j--){
            dp[j]=max(dp[j],dp[j-a[i]]+a[i]);
            //因为“重量、价值”一样，所以减得a[i]和加的a[i]一样。
        }
    }//简直一毛一样，不用多说了吧。
    cout<<dp[he/2]*(he-dp[he/2]);
    //唯一要思考的，面积=长*宽，dp[he/2]就是长，he-dp[he/2]就是宽（宽=总长-长）。
    return 0;
}

木棍搭边

原理

为什么会导致面积不同呢？由于我们希望面积最大，所以一定会把所有的木棍都搭进长或宽里，所以长和宽的和一定是所有数之和，但是面积还是有大有小。这是因为“和一定差小积大”，我们需要让长和宽相差最小。

第一种想法

为了让差最小，所以乍一看每次都要让长宽较短的加上下一个数就可以了。但是这是有问题的。 按照输入的顺序，"2 3 4"，这样算下来是 $6 \times 3 = 18$ 并不是最大的。

第二种想法

让差最小，也相当于让长尽量接近总长的一半，我们可以使用01背包。