题解

思路1

这道题一上来就可以暴力，常言道“暴力出奇迹，骗分过样例。”，如果比赛时不会没时间数学推导，就只能暴力。

这道题正解是递归，我们观察一下 $5 \times 5$ 和 $6 \times 6$ 的方阵（代表奇数和偶数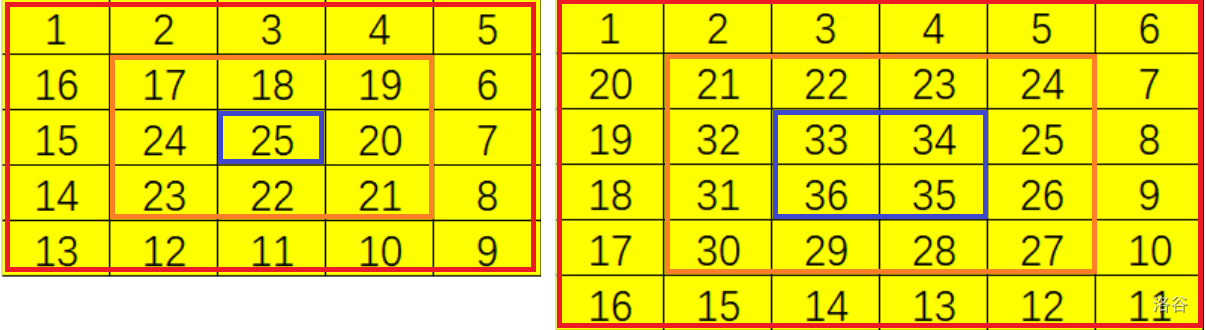）： 无论是奇数还是偶数，他的子矩阵（指向中心缩小一圈的子矩阵）总是也符合螺旋矩阵的要求，所以我们想到了递归：

int search(int n, int i, int j); // 表示n * n的螺旋矩阵中(i, j)的数字

用 search 函数表示 $n \times n$ 的螺旋矩阵中 $(i, j)$ 的数字。

我们再次观察矩阵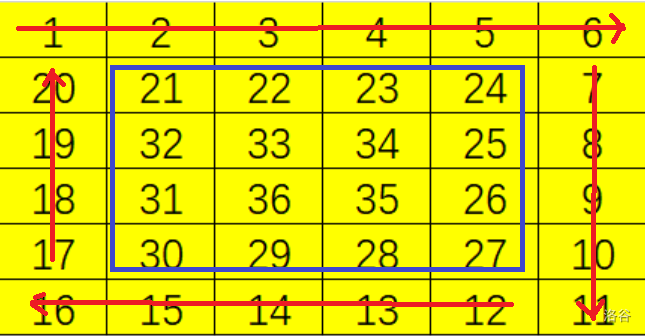： 这时我们可以特判 $(i, j)$ 位于这几部分中那一部分：如果在箭头部分上，就根据这一圈第几个算数字；如果在内部，就直接递归。

这里我们列出情况：

1. 位于上面：此时 $i = 1$，数字为 $j$。
2. 位于右面：此时 $j = n$，数字为 $n - i + 1$。
3. 位于下面：此时 $i = n$，数字为 $3 \times n - 2 - j + 1$。
4. 位于左面：此时 $j = 1$，数字为 $4 \times n - 4 - i + 2$。 $\$

• 啥也不是：此时都不符合，答案为 $search(n - 2, i - 1, j - 1) + 4 \times (n - 1)$。

位于某个方面这里先不详细讲了，重点在怎么来的：

我们知道，内部也符合螺旋结构，可以复用递推。可是下一层的 $n$ 是 $n - 2$ 而非 $n - 1$，因为小了一圈少左右两边。这里 $i, j$ 各自 $- 1$ 以适应下一层的坐标系。可是这个 $4 \times (n - 1)$ 是哪里来的？其实很简单，我们的 search 函数返回的都是 $j$，$n - i + 1$ 这种，没有考虑内层开头就不是 $1$ 了（见图），这是我们通过 $4 \times (n - 1)$ 计算出下一层的起头，这样就可以了。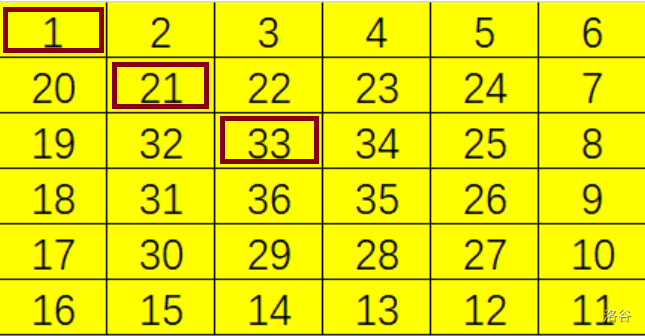

这样写出 search 函数。

int search(int n, int i, int j) // 表示n * n的螺旋矩阵中(i, j)的数字
{
    if (i == 1) // 上
    	return j;
    if (j == n) // 下
    	return n + i - 1;
    if (i == n) // 左
    	return 3 * n - 2 - j + 1;
    if (j == 1) // 右
    	return 4 * n - 4 - i + 2;
    return search(n - 2, i - 1, j - 1) + 4 * (n - 1); // 递归内部
}

答案就是 search(n, i, j)，补全程序即可：

#include <bits/stdc++.h>
using namespace std;
int n, i, j;
int search(int n, int i, int j) // 表示n * n的螺旋矩阵中(i, j)的数字
{
    if (i == 1) // 上
    	return j;
    if (j == n) // 下
    	return n + i - 1;
    if (i == n) // 左
    	return 3 * n - 2 - j + 1;
    if (j == 1) // 右
    	return 4 * n - 4 - i + 2;
    return search(n - 2, i - 1, j - 1) + 4 * (n - 1); // 递归内部
}
int main()
{
    // 答案就是 search(n, i, j)
    scanf("%d%d%d", &n, &i, &j);
    printf("%d\n", search(n, i, j));
    return 0;
}

思路2

暴力做法是填表模拟（MLE/TLE），其实模拟也可以AC。

其实，模拟根本就不需要开 $30000 \times 30000$ 的数组。考虑到它是求第 $i$ 行第 $j$ 列的数，其实我们可以只针对第 $j$ 列的数，进行填数模拟，这样时间复杂度就降到了 $O(n)$ 了，也不会爆。模拟其实也很简单，就是向右绕半圈，向左绕半圈，直到行等于 $i$ 时跳出就可以了。

另外，如果这样模拟，就会有一个坑点难以想到。有时候，可能绕的这半圈已经变成了一条直线了，这样这第 $i$ 行的数就可能在这条直线中，则必须加一个特判，加上上一个点到终点的距离，然后就得跳出了。如果不加特判，程序继续运行，模拟便会出错，然后就只有 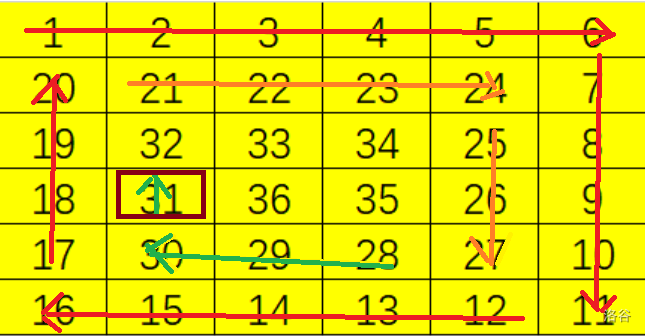$60pts$ 了…… 代码：

#include <bits/stdc++.h>
#define left ___left // 因为left、right变量名可能和库里定义的东西撞名了，这里为了方便理解，#define去除一下
#define right ___right
using namespace std;
int n, x, y;
int rx, num, top, bottom, left, right; // 当前行数rx，目前的数num // 上下左右一圈边界
int d; // 方向 0上 1下
int main()
{
    scanf("%d%d%d", &n, &x, &y);
    // 初始化
    rx = 1, num = y;
    top = 1, bottom = n, left = 1, right = n;
    d = 1; //方向初始向下
    while (rx != x) //一直模拟到刚好到达
    {
        if (d) // 向下
        {
            if (right == y) // 如果是往下走直线
            {
                num += x - rx;
                break;
            }
        }
        else // 向上
        {
            if (left == y) //如果是向上走直线
            {
                num += rx - x;
                break;
            }
        }
        if (d) //普通情况向下走
        {
            num += (right - y + 1) * 2 + bottom - rx - 2; //绕一圈
            rx = bottom; //更新所在的行
            right--; //右边界往回退一格
            top++; //上边界往回退一格
        }
        else //往上走
        {
            num += (y - left + 1) * 2 + rx - top - 2; //绕一圈
            rx = top; //更新行
            left++; //左边界回退
            bottom--; //下边界回退
        }
        d = 1 - d; //方向调转
    }
    printf("%d\n", num);
    return 0;
}

$AC$ $Code$ $1$

#include <bits/stdc++.h>
using namespace std;
int n, i, j;
int search(int n, int i, int j)
{
    if (i == 1)
    	return j;
    if (j == n)
    	return n + i - 1;
    if (i == n)
    	return 3 * n - 2 - j + 1;
    if (j == 1)
    	return 4 * n - 4 - i + 2;
    return search(n - 2, i - 1, j - 1) + 4 * (n - 1);
}
int main()
{
    scanf("%d%d%d", &n, &i, &j);
    printf("%d\n", search(n, i, j));
    return 0;
}

$AC$ $Code$ $2$

#include <bits/stdc++.h>
#define left ___left
#define right ___right
using namespace std;
int n, x, y;
int rx, num, top, bottom, left, right;
int d;
int main()
{
    scanf("%d%d%d", &n, &x, &y);
    rx = 1, num = y;
    top = 1, bottom = n, left = 1, right = n;
    d = 1;
    while (rx != x)
    {
        if (d)
        {
            if (right == y)
            {
                num += x - rx;
                break;
            }
        }
        else
        {
            if (left == y)
            {
                num += rx - x;
                break;
            }
        }
        if (d)
        {
            num += (right - y + 1) * 2 + bottom - rx - 2;
            rx = bottom;
            right--;
            top++;
        }
        else
        {
            num += (y - left + 1) * 2 + rx - top - 2;
            rx = top;
            left++;
            bottom--;
        }
        d = 1 - d;
    }
    printf("%d\n", num);
    return 0;
}

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll n, i, j;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n >> i >> j;
    ll l = min(i, min(n - i + 1, min(j, n - j + 1))); // 处在第几圈
    ll x = 4 * (l - 1) * (n - l + 1);                 // 上一圈的结尾
    if (i == l)
        x += j - l + 1;
    else if (j == n - l + 1)
        x += n - 3 * l + 2 + i;
    else if (i == n - l + 1)
        x += 3 * n - 5 * l + 4 - j;
    else
        x = 4 * l * (n - l) + (l - i + 1);
    cout << x;
    return 0;
}

数学题找规律