可以看出这个题就是求一棵代价最小的生成树，由于边权要乘以高度的缘故，所以不能初始求一遍普通的生成树，但是前 $20$ 分保证是一棵树，所以可以直接暴力求解，即枚举每个点作为起点开拓一次搜索一次树

考虑状压 DP 求解

状态设计：$f_{i,j}$ 当前已经加入的点的集合是 $i$ 当前树的高度是 $j$ 的所有方案。

答案：$\min_{i=1}^{n-1} (f_{2^n-1,i})$

状态转移：考虑上一个不同的状态必然是由 $f_{s, j-1}$ 加入了部分点到第 $j$ 层后得到 $f_{i,j}$

这里我们来证明一下，为何一定要将部分点加入到第 $j$ 层而不需要考虑这部分点加入到前面的每一层来去求一个最小值。

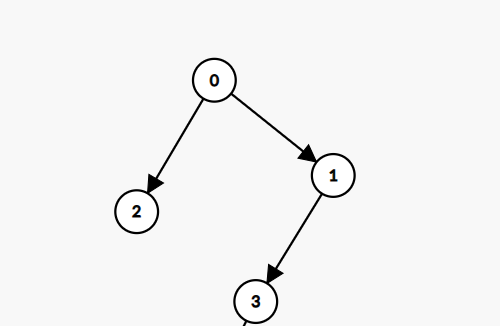
如下图新加入的点 $4$ 我们直接连到最后一层。

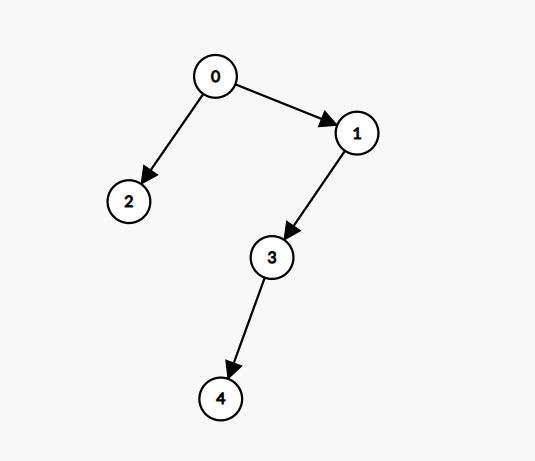
如果点 $4$ 是连接到更上的一层的答案比连接到下面的答案更优，那么我们在之前肯定已经枚举过这种状态并计算过答案了。因为我们的状态设计是 $f_{i,j}$ 其含义是当前已经加入的点的集合是 $i$ 当前树的高度是 $j$ 的所有方案.在之前的高度我们是已经计算过点 $4$ 去到低的层的情况，因而再求新的情况我们不需要再去考虑之前的情况，这样是不会漏算的。

具体来说：

• 枚举所有的状态 $i$
• 枚举状态 $i$ 的子集 $k$ 考虑将这一部分点加入到新的一层 $j$，那么 i ^ k 就是前 $j-1$ 层的点集，这一部分的答案是 $f_{i\oplus k,j-1}$
• 因此只需要累加点集 $k$ 加入到点集 $i\oplus k$ 的最小权值即可。这一部分我们可以首先预处理每个点到任意点集的最小距离，然后总距离和乘以树的高度就是这一部分的代价。

时间复杂度： $O(3^n*n)$

枚举所有的子集，在枚举子集的子集，这个复杂度是 $O(3^n)$ 的，还需要枚举树的高度这是 $O(n)$ 的

浅显的证明一下枚举所有的子集，在枚举子集的子集，这个复杂度是 $O(3^n)$

我们容易知道一个大小为 $n$ 的集合，它一共有 $2^n$ 个子集，那么每一个子集有多少个子集呢？

子集个数可以用如下式子表示

$\sum_{k=0}^n C_n^k$ 即从 $n$ 个元素中选择 $k$ 的所有方案。每一个子集含有 $k$ 个元素，则这一部分的子集是 $2^k$

故枚举子集的子集一共有 $\sum_{k=0}^n C_n^k\times 2^k$

根据二项式定理， $(a+b)^n=\sum_{i=0}^n C_n^i a^{n-i}*b_i$

可得$\sum_{k=0}^n C_n^k\times 2^k=\sum_{k=0}^n C_n^k 1^{n-k}\times 2^k=(1+2)^n=3^n$

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 12, M = 1 << N;
int n, m, dis[N][N];
int f[M][N], g[N][M];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0); 
    cin >> n >> m;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            if (i != j) dis[i][j] = 1e9;
    for (int i = 1; i <= m; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        u--, v--;
        dis[u][v] = dis[v][u] = min(dis[u][v], w);
    }
    memset(g, 0x3f, sizeof(g));
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < (1 << n); j++)
        {
            for (int k = 0; k < n; k++)
            {
                if (j >> k & 1)//集合 j 里含有 k
                {
                    g[i][j] = min(g[i][j], dis[i][k]);//更新点 i 到集合 j 的最小距离是点i到k的距离
                }
            }
        }
    }
    memset(f, 0x3f, sizeof(f));
    for (int i = 0; i < n; i++) f[1 << i][0] = 0;//初始化开拓点 i 且高度为 0 的情况代价为 0
    for (int i = 1; i < (1 << n); i++)//枚举所有的状态
    {
        for (int k = i - 1 & i; k; k = k - 1 & i)//枚举集合 i 的子集 k
        {
            int r = i ^ k;
            int cost = 0;
            for (int j = 0; j < n; j++)
            {
                if (k >> j & 1)
                {
                    if (cost >= 1e9) continue;
                    cost += g[j][r];
                }
            }
            if (cost >= 1e9) continue;
            for (int j = 1; j < n; j++) f[i][j] = min(f[i][j], f[r][j - 1] + cost * j);
        }
        
    }
    int res = 1e9;
    for (int i = 0; i < n; i++) res = min(res, f[(1 << n) - 1][i]);
    cout << res;
    return 0;
}