霍夫曼树

树的带权路径长度

设二叉树具有 nn个带权叶结点，从根结点到各叶结点的路径长度与相应叶节点权值的乘积之和称为 树的带权路径长度（\text{Weighted Path Length of Tree，WPL}Weighted Path Length of Tree，WPL）。

设w_iwi​为二叉树第ii 个叶结点的权值，l_ili​ 为从根结点到第 ii 个叶结点的路径长度，则 \text{WPL}WPL 计算公式如下：

WPL=\sum_{i=1}^nw_il_iWPL=i=1∑n​wi​li​

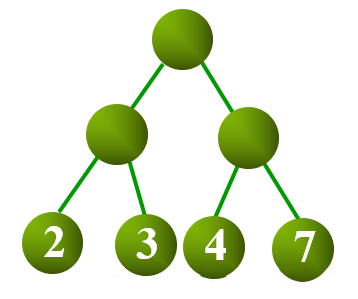
如上图所示，其 \text{WPL}WPL 计算过程与结果如下：

WPL=2*2+3*2+4*2+7*2=4+6+8+14=32WPL=2∗2+3∗2+4∗2+7∗2=4+6+8+14=32

对于给定一组具有确定权值的叶结点，可以构造出不同的二叉树，其中，\text{WPL}WPL 最小的二叉树 称为 霍夫曼树（\text{Huffman Tree}Huffman Tree）。

对于霍夫曼树来说，其叶结点权值越小，离根越远，叶结点权值越大，离根越近，此外其仅有叶结点的度为 00，其他结点度均为 22。

霍夫曼算法

霍夫曼算法用于构造一棵霍夫曼树，算法步骤如下：

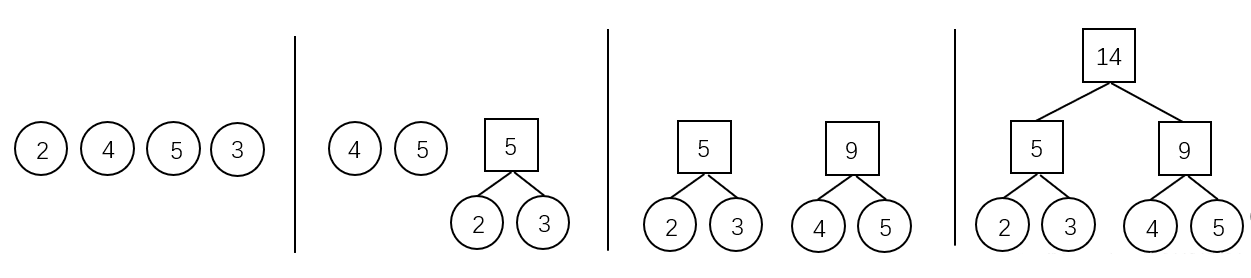
1. 初始化：由给定的 nn 个权值构造 nn 棵只有一个根节点的二叉树，得到一个二叉树集合FF。
2. 选取与合并：从二叉树集合 FF 中选取根节点权值 最小的两棵 二叉树分别作为左右子树构造一棵新的二叉树，这棵新二叉树的根节点的权值为其左、右子树根结点的权值和。
3. 删除与加入：从 FF 中删除作为左、右子树的两棵二叉树，并将新建立的二叉树加入到 FF 中。
4. 重复 22、33 步，当集合中只剩下一棵二叉树时，这棵二叉树就是霍夫曼树。

霍夫曼编码

在进行程序设计时，通常给每一个字符标记一个单独的代码来表示一组字符，即 编码。

在进行二进制编码时，假设所有的代码都等长，那么表示nn 个不同的字符需要 \left \lceil \log_2 n \right \rceil**⌈log2​n**⌉位，称为 等长编码。

如果每个字符的 使用频率相等，那么等长编码无疑是空间效率最高的编码方法，而如果字符出现的频率不同，则可以让频率高的字符采用尽可能短的编码，频率低的字符采用尽可能长的编码，来构造出一种 不等长编码，从而获得更好的空间效率。

在设计不等长编码时，要考虑解码的唯一性，如果一组编码中任一编码都不是其他任何一个编码的前缀，那么称这组编码为 前缀编码，其保证了编码被解码时的唯一性。

霍夫曼树可用于构造 最短的前缀编码，即 霍夫曼编码（\text{Huffman Code}Huffman Code），其构造步骤如下：

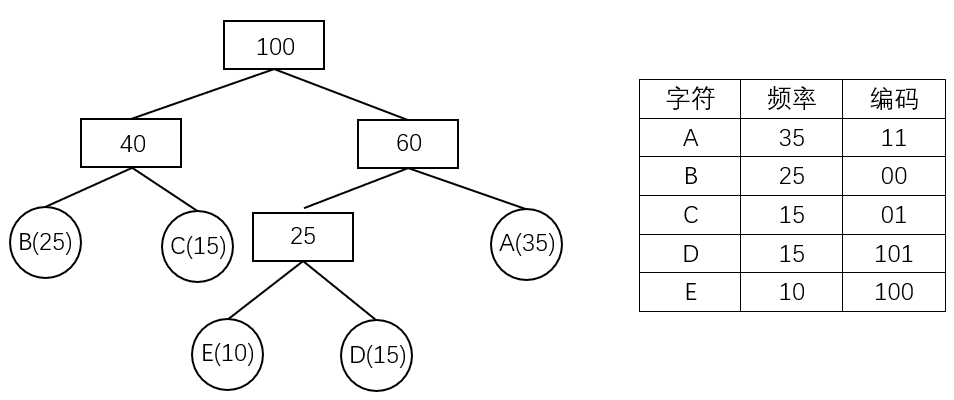
1. 设需要编码的字符集为：d_1,d_2,\dots,d_nd1​,d2​,…,dn​，他们在字符串中出现的频率为：w_1,w_2,\dots,w_nw1​,w2​,…,wn​。
2. 以 d_1,d_2,\dots,d_nd1​,d2​,…,dn​ 作为叶结点，w_1,w_2,\dots,w_nw1​,w2​,…,wn​ 作为叶结点的权值，构造一棵霍夫曼树。
3. 规定哈夫曼编码树的左分支代表 00，右分支代表 11，则从根结点到每个叶结点所经过的路径组成的 00、11 序列即为该叶结点对应字符的编码。

例题

荷马史诗

这个题不难看出是 kk 叉哈夫曼树，那么 kk 叉哈夫曼树在构造的时候，大体和我们二叉是一样的，不难发现二叉就是每次选两个权值最小的点，然后生成一个新的节点，然后继续寻找这个过程，很想合并果子那个题？

这里 kk 叉哈夫曼树也类似，不过有一些特例，这里我们等价于每次一定选择 kk 个节点，然后生成一个新节点，但是有可能剩余的节点不够kk个，导致无法选择？

这个时候容易发现，继续按照这个思路贪心是可以举出反例的，因为我们可以把前面构造好的权值大的点，拉上来降低深度，就降低了 WPLWPL.

所以正确做法是首先判断 (n-1)\%(k-1)(n−1**)%(k−1)** 是否等于 00。

解释：

首先我们每次选 kk 个，然后生成一个，相当于每次减少 k-1k−1 个点，为何是 n-1n−1 ，因为最后那个点当根节点去了，不需要再进行新一轮选择。

那么如果不等于 00 ，我们可以人为的添加一些权值为 00 的点，以此满足 (n-1)\%(k-1)0**(n−1)%(k−1)**0 ,那么添加多少呢？

不难计算出是 k-1-modk−1−mod,modmod 就是上面式子的余数。