#P3058. [COCI2020-2021#1] Papričice
[COCI2020-2021#1] Papričice
题目描述
给定一个 个点的树,这 个点编号为 到 。
现在要选择断掉两条边,会形成三个连通块,假设这三个连通块内的点数分别为 ,那么您要做的就是最小化 的大小,求这个最小值。
输入格式
第一行一个整数 代表树的点数。
接下来 行每行两个整数 代表树的一条边。
输出格式
一行一个整数代表答案。
4
1 2
2 3
3 4
1
6
1 2
1 3
3 4
3 5
5 6
0
9
1 3
2 3
3 4
3 5
5 6
5 7
7 8
7 9
2
提示
样例 1 解释
能构造的最优解三个连通块的点数都为 ,所以输出 。
样例 2 解释
断掉点 到点 的边,点 到点 的边,形成的三个连通块点数相同。
样例 3 解释
如下图所示:
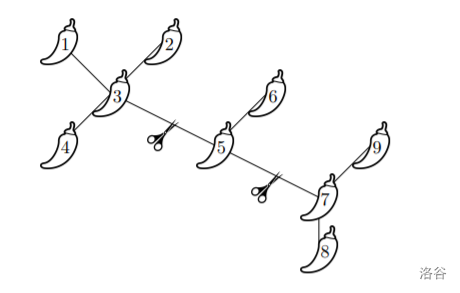
数据规模与约定
本题采用捆绑测试。
- Subtask 1(15 pts):。
- Subtask 2(35 pts):。
- Subtask 3(60 pts):。
对于 的数据,。
本题满分 分。
说明
翻译自 Croatian Open Competition in Informatics 2020 ~ 2021 Round 1 D Papričice 。
