题目描述

某校有 $N$ 间教室，且每间教室有 $2$ 扇门，一共有 $2 \times N$ 扇门，每扇门都有编号，分别从 $1$ 到 $2 \times N$。

开始时，所有门为关闭状态。现在按照以下规则对门进行处理：

第一次，将所有的门打开；

第二次，将所有编号为 $2$ 的倍数的门作相反的处理（原来是打开的就关闭，原来是关闭的就打开）；

第三次，将所有编号为 $3$ 的倍数的门作相反的处理（原来是打开的就关闭，原来是关闭的就打开）；

以此类推；

第 $N$ 次，将所有编号为 $N$ 的倍数的门作相反的处理（原来是打开的就关闭，原来是关闭的就打开）。

问第 $N$ 次处理后，有多少扇门为打开状态？

例如：$N=2$，每间教室有 $2$ 扇门，一共有 $4$ 扇门，门编号分别为 $1$、$2$、$3$、$4$

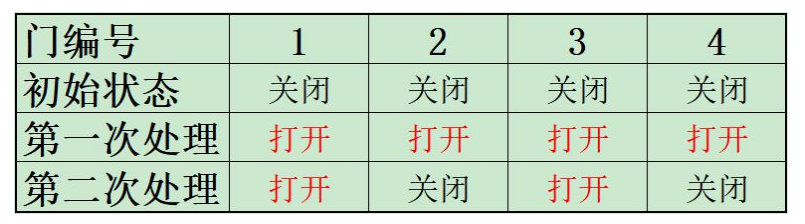
初始状态：四扇门都为关闭状态；

第一次，将四扇门全部打开；

第二次，将编号为 $2$ 的倍数的门作相反的处理，即将 $2$ 号门和 $4$ 号门关闭。

经过两次处理之后，共有 $2$ 扇门为打开状态。

如下图：

输入格式

输入一个正整数 $N(2 \le N \le 100)$，代表有 $N$ 间教室。

输出格式

按照规则对门进行 $N$ 次处理之后，计算有多少扇门为打开状态并输出。

2

2

10

12